无锡市环球教育培训中心 张云帆

在申请北美本科留学时，多数学校更注重考生 SAT I 考试的阅读和数学这两个部分的成
绩。虽然阅读部分胜似一道难以逾越的鸿沟，可数学部分对于广大大陆考生而言，可谓是小
菜一碟；摆在眼前的事实却是，鲜有考生答对全部的 54 题、如愿获取满分。究其原因，无
非是两个字：轻敌。对此，笔者有如下三条建议。

重视平时定期练习、及时归纳总结错题
SAT I 数学部分的难度及深度远不如国内的高中教育，因此考生对于 SAT I 的数学部分
便有了一种先入为主的错误看法：随便一考就是 800 分。可是历届考试的结果来看，栽在数
学部分的考生不在少数，撇去考试难度逐年递增这一客观原因不谈，主要原因还在于考生对
于 SAT I 数学不够重视的态度。平时应该注重 SAT I 数学的定期练习，不需要大量的做题，
但是必须保证每次都完成一整套 3 个 SECTION 的训练。这些练习本身是有意义的，而且可
以作为复习阅读和写作部分的调剂，所谓的“换换脑子”。另外，在练习的过程中，难免会
出现一些难题、错题，此时及时做好整理工作“有百利而无一害”。
以下为两例常见错题

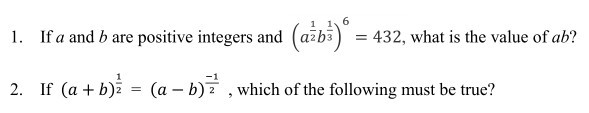
A. b = 0
B. a + b = 1
C. a - b = 1
D. a2 + b2 = 1
E. a2 - b2 = 1

考试中间认真审题、注意避开答题陷阱
通常SAT I数学考查的知识点并不困难，但是会在提问时设置陷阱。比如应用题中的单
位转换，条件中给出的单位是inch，但最后结果要求以foot表示。再比如，2012年10月真题
中一道求总费用的应用题，要按不同小时段不同收费方式计算，下午13时至18时这个时段一
共是6小时，如果按18 -13 = 5小时计算的话，就会造成无谓的失分。此外，还要重视一些英
文理解，例如,谁比谁多、谁是谁的几倍这些类似的表达都是考生需要熟记的。
以下两例均设有陷阱：
1. The least integer of a set of consecutive integers is -25. If the sum of these integers
is 26, how many integers are in this set?
2. The pattern shown below is composed of rectangles. This pattern is used repeatedly
to completely cover a rectangular region 12L units long and 10L units wide. How
many rectangles of dimension L by W are needed?